
Análisis de la carta topográfica de la zona de la Estancia Monte Dinero.
Investigación y trabajo de campo:
Expedición Costera (1980-81)
Roberto Hilson Foot
Expedición Ea. Condor – Rio Gallegos (Enero 1990)
Ing. Agr. Horacio Cerutti
Roberto Hilson Foot.
Expedición Costera (2003)
Pía Simonetti
Daniel Bruno
Lucas Young
Juan Manuel Botello
Roberto Hilson Foot
Fotografías:
Juan Manuel Botello (2003)
Roberto Hilson Foot (2003)
Agradecimientos:
A la familia Fenton de la Estancia Monte Dinero. A los miembros de la cátedra de Cartografía de la Facultad de Filosofía y Letras, UBA.
I
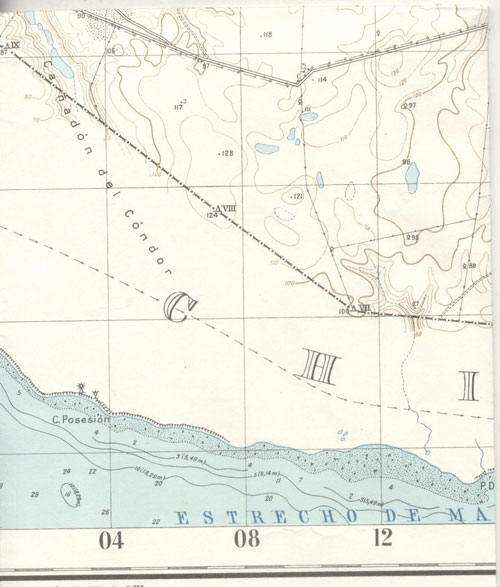
Nos proponemos en este artículo analizar la hoja 5369-4, denominada Monte Dinero, de la provincia de Santa Cruz. Esta carta topográfica fue levantada en el año 1942, tiene una escala de 1:100.000, con una equidistancia de 10 metros. Podemos ubicar esta zona en el extremo sur continental en la frontera con Chile entre los 52° 00´ y los 52° 20´ de latitud sur, en el departamento de Güer Aike.
II
La escala del mapa tal como adelantamos es de 1:100.000. Cuando nos referimos a la escala estamos expresando una proporción o razón entre el mapa y el terreno. Es por tanto un valor numérico que implica un grado de reducción de las medidas lineales. Siendo el mapa una representación gráfica de un territorio debe mediar una correspondencia en la proporción entre el signo y su referencia semántica.
En esta carta 1cm en el plano corresponden a 100.000 cm. en el terreno. En el sistema métrico decimal tenemos como unidades los kilómetros, hectómetros, decámetros, metros, decímetros, centímetros, milímetros, etc. Por lo tanto 100.000cm son 1000m o lo que es lo mismo 1 km. En esta hoja por tanto 1cm sobre el plano corresponde a 1 km en el terreno.
Si medimos por ejemplo la distancia entre el Hito Internacional VII y el Hito Internacional VIII nos da un valor de 5cm sobre la hoja.
Aplicando la formula:
1/D = P/T despejamos y D x P=T
por lo tanto
100.000 x 5cm = 500.000cm
Lo que es igual a 5.000m
Por ende la distancia en el terreno entre el Hito VII y el Hito VIII es de 5.000m o 5Km.

En el caso de medir líneas curvas, uno debe descomponer la curva en segmentos mas cercanos a la recta haciéndolos mensurables. Si medimos la longitud de la línea de costa o sea la línea azul que representa los 0 m.s.n.m. obtendremos un valor de 24,6cm para el frente Atlántico, lo cual de acuerdo a la escala representa 24,6Km que sumados a los 28,4km de costa Atlántica de la hoja 5369-5 Cabo Vírgenes suma un total de 53,0 Km. de costa entre los dos mapas.
Con respecto a las escalas cuadráticas o de superficie en la hoja en 1:100.000 cada uno de los lados del cuadrado de la cuadrícula de coordenadas planas tiene 4cm por lo que corresponde a 4Km. Ello implica un área de 16cm2 en la hoja que corresponden a 16km2 en el terreno.
Una escala de 1:100.000 puede ser clasificada como de escala media, siendo las escalas grandes las que tienen pequeños denominadores, por ejemplo 1:50.000 o 1:25.000, mientras las escalas pequeñas tienen grandes denominadores, por ejemplo 1:500.000 o 1:1.000.000. El adjetivo de grande o pequeño está en función del nivel de detalle, pues recordemos que la escala elegida determina el nivel de análisis.
III
En la parte inferior de la hoja, podemos encontrar los signos cartográficos de uso mas frecuente.
Dichos signos son representaciones gráficas de objetos, siendo el simbolismo cartográfico como su misma denominación lo indica una organización convencional. Esa semiología gráfica tiene tres modos de implantación:
Puntual, por ejemplo el mojón o hito.
Lineal, por ejemplo un camino.
Areal o Zonal, por ejemplo una laguna temporal.
Estos signos o símbolos convencionales presentan por lo menos seis variables gráficas a saber:
Forma
Tamaño-dimensión
Orientación
Color y tonalidades
Intensidad y gradación
Estructura de la mancha
Esta semiología gráfica pretende ser un lenguaje monosémico, racional y operativo, concebido como un lenguaje universal en donde la polisemia puede ser atenuada o reducida en su denotación.
IV

Con respecto al complejo problema de cómo representar un objeto que tiene tres dimensiones como es la tierra en un plano con dos dimensiones, la hoja estudiada es parte de la larga tradición que remite a Mercator.
Gerardo Kremer, cuyo apellido latinizado era Mercator fue un geógrafo flamenco nacido en Rupelmonde en 1512 quien inventó en 1569 la proyección que lleva su nombre. Su obra gozó de gran éxito pues permitía fijar rumbos al mantener el valor de la latitud y longitud de cada punto sacrificando la forma de los continentes.
La proyección de Mercator es cilíndrica, lo cual significa que se utiliza un cilindro cuyo eje es perpendicular al plano del ecuador como figura geométrica a desarrollar sobre un rectángulo con los paralelos y meridianos ortogonales y rectilíneos.
La línea ecuatorial esta representada sin distorsiones, pero la prolongación en la extensión de los paralelos esta compensada por una exageración proporcional de las distancias meridianas. Ello se hace por medio de una función denominada variable de Mercator, o de las latitudes crecientes.
La proyección es por lo tanto conforme, pero con la latitud varía la escala generando una distorsión en las formas.
Durante los siglos XVIII y XIX se creó y desarrolló una variante denominada transversa de Mercator, con un cilindro como había utilizado el geógrafo en el siglo XVI pero tangente a un meridiano, en vez de la tangencia con la línea ecuatorial.
En la Argentina a los fines geodésicos y cartográficos, se adoptó el elipsoide de Hayford en 1920 con un radio ecuatorial de 6378,388km., y un valor de flattering (f) de 1 en 297. A este elipsoide se le aplica la UTN, Universal Transversa de Mercator, en la versión elaborada por Gauss y Kruger.
Cal Friedrich Gauss (1777-1856) quien, siendo hijo de una familia humilde, por su gran talento en matemáticas, fue protegido por el Duque de Brunswick, lo cual le permitió estudiar en Gotinga y luego doctorarse en la universidad de Helmstedt, siendo desde 1807 director del observatorio de Gotinga. En 1821 elabora el mapa del estado Hanover con proyección transversa siendo un pionero en su aplicación.
Su trabajo sería completado en Potsdan en 1912 por el Dr. Louis Kruger con un sistema de proyección transversa cilíndrica con fajas. En el caso de la Argentina se aplico este criterio determinando siete fajas que corresponden a siete medianos de tangencia con un ancho de 3° de longitud de cada uno. Desde la faja 1 para el meridiano 72° W hasta la faja 7 para el meridiano de 54° W se cubre todo el ancho del país.
Si observamos la hoja 5369-4 en el ángulo superior izquierdo podemos observar los números 2492 y luego 2500 que corresponden al meridiano de 69°00´. Este meridiano es el de tangencia de la segunda faja en la proyección Gauss Kruge, y el primer numero de la serie, el dos, indica esto precisamente, el ser la segunda faja.
Si a continuación observamos los números sobre la margen izquierda y derecha del mapa podemos leer también los valores correspondientes a las coordenadas planas, por ejemplo 4204 lo cual significa que en esa ubicación (apenas a 1.000m de Ea.Monte Dinero) uno se encuentra a 4204Km del Polo Sur, tomándose a este punto como valor 0 y creciendo numéricamente en dirección al ecuador.
Bibliografía
Estrada Espinosa de los Monteros, José M., “Laboratorio de cartografía“, Editorial Trillas, 1988.
Gillett, Jack, “Mapwork Skills and Local Issues“, Hodder and Stoughton, 1998.
Instituto Geográfico Militar, “Lectura de Cartografía.” I.G.M., 1984.
Instituto Geográfico Militar, “Curso técnico del Servicio Geográfico. Topografía.” I.G.M. 1980.
Joly, Fernand, “La Cartografía. Oikos Tau“, España. 1988.
Magnani, E., “Divagaciones cartográficas a propósito de un mapa chino.” Diario Página 12, Julio 1998.